2022年1月13日发表在Nature Biotechnology上的 《Cell2location maps fine-grained cell types in spatial transcriptomics》其实是一个很久的工作了,最早在20年应该就能在github上找到。之前也有零星的中文资料对这个工作进行了介绍,比如
10X单细胞和空间联合分析的方法---cell2location - 简书 (jianshu.com)
可惜和大多数生信分析的教程一样,可能是为了照顾相当一部分生物出身的读者,对模型的建模和细节都没有讲。而这篇文章的概率图模型又比较复杂,是多层次的。我来尝试梳理一下,也欢迎各位同僚在评论区讨论。
这个模型总体是为了解决所谓的解卷积问题,也就是将空间测序中的一个spot解成多个细胞类型的加权组合。这个问题反过来看,就是寻找某一个细胞类型在空间上最有可能出现的位置的频率分布,也就是将cell to location,我猜也是工具名字的来源。
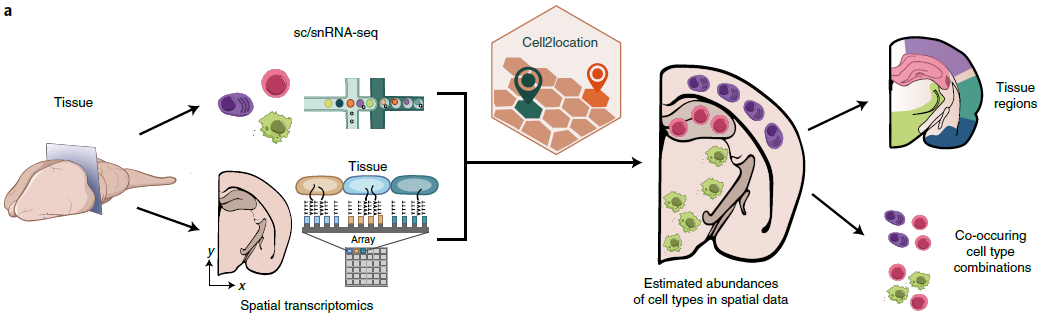
模型总的流程图如下所示,这篇文章的实从同一个组织区域同时进行了单细胞还有空间测序,利用这样的配对数据帮助空间转录组划分解剖区域和解卷积,另一方面也定位了单细胞在空间中的位置,并找到了最有可能的细胞类型共表达模式。注意这里的细胞类型共表达模式是文章以及数据建模中比较重要的一个概念,作者在文章附件也提到通过考虑表达模式是他们方法能找到精细结构非常重要的原因,也是这篇工作和其他直接进行解卷积工作的区别之处。
接下来我们直接进入方法部分,首先这是作者模型的概率图模型,是不是很复杂,但等你读完这篇文章,会发现这个图其实画的非常清晰易懂,还可以帮助你加深记忆。
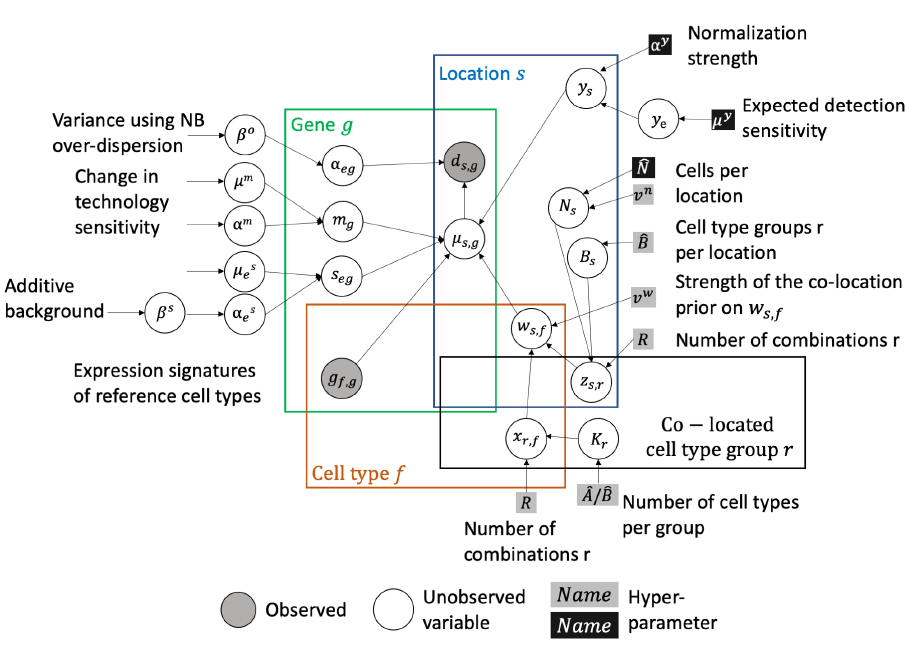
我们一步步来推导。首先,作者约定空间转录组数据矩阵$D=\{d_{s,g}\}$为$S \times G$的矩阵,其中$S$为空间位置的总数,$G$为基因数,这些空间位置来自于不同的batch,而batch的总数为$E$。单细胞测序得到的细胞类型参考矩阵$G=\{g_{f,g}\}$为$F \times G$的矩阵,其中$F$为细胞类型的个数,$G$为基因数。这个矩阵就是将原来的单细胞矩阵按照不同细胞类型的归属求取了平均值得到的。
这里注意到两个矩阵的基因数必须要保证是一样的,但作者没有说明如果单细胞与空间转录组基因数不对齐的话需要用什么办法进行统一。
然后作者就开始进行建模了。对于每个空间转录组位点里基因g的counts数,作者认为其服从负二项分布,其中均值参数为$\mu_{s,g}$,dispersion参数为$\alpha_{e,g}$:
$d_{s,g} \sim NB(\mu_{s,g}, \alpha_{e,g}) \qquad (1)$
而之所以要建模成负二项分布,一个是从经验上发现符合空间转录组数据特征外,还有就是从理论上,测序技术对于游离的mRNA进行捕获时,得到的counts数可以理解为是从一个概率比较低(p很小),但是次数很多的(n很大)的二项分布中采样得到的,而这样的二项分布我们可以用泊松分布进行代替。但这样做的一个问题是泊松分布的均值和方差是一样的,这和实际情况又不是很相符,于是对于泊松分布的参数$\lambda$我们可以认为它服从Gamma分布。这样我们就得到了Poisson-Gamma混合分布,而这样的分布本质上就是负二项分布(详情证明见17. 负二项式模型 — 张振虎的博客 张振虎 文档 (zhangzhenhu.github.io))
所以,公式(1)可以写作:
$d_{s,g} \sim Poisson(Gamma(\alpha_{e,g}, \alpha_{e,g} /\mu_{s,g})) \qquad (2)$
注意这里作者用的是应该是$Gamma(\alpha,\theta)$的形式,也就是说,均值为$\alpha / \theta$,代入到上面的式子中,均值是$\mu_{s,g}$,和公式1相等。对于这两个参数,作者又用了层次化的建模方法:
参数$\mu_{s,g}$
对于参数$\mu_{s,g}$,其服从以下建模:
$$
\mu_{s, g}=(\underbrace{m_{g}}_{\text {technology sensitivity }} \cdot \underbrace{\sum_{f} w_{s, f} g_{f, g}}_{\text {cell type contributions }}+\underbrace{s_{e, g}}_{\text {additive shift }}) \cdot \underbrace{y_s}_{\text {per-location sensitivity }} \qquad (3)
$$
其中$ w_{s, f}$可以看作是每个细胞类型$f$在位置$s$上的回归权值,可以理解为细胞类型$f$在位置$s$的绝对细胞丰度(absolute cell abundance)
其中$m_g$代表基因特异的尺度因子,描绘的是宏观上不同平台带来的测序量的影响。
其中$s_{e,g}$代表数据中的加性偏移,比如游离的RNA
其中$y_s$是位置特异的检测效率尺度因子,描绘的是不同位置上对于捕获RNA的灵敏度差异。
你问我其中的$g_{f,g}$是什么?建议重新找一个安静的时间段再来读这篇方法讲解。我开头的方法部分写的很清楚了。是细胞类型参考矩阵里第f个细胞类型中g基因的表达值。
那么这些参数本身肯定还服从一个概率分布,否则怎么能算得上多层次概率图模型呢(手动狗头)
细胞类型在不同位置的绝对丰度:参数$w_{s,f}$
首先这个参数服从Gamma分布:
$$
w_{s, f} \sim \operatorname{Gamma}\left(\mu_{s, f}^{w} v^{w}, v^{w}\right) \qquad (4)
$$
其中的参数$v^{w}$是一个固定的超参数,来控制先验的强度。而参数$\mu_{s, f}$是由$R$个潜在的细胞类型分组线性加和而成的:
$$
\mu_{s, f}^{w}=\sum_{r} z_{s, r} x_{r, f} \qquad (5)
$$
算法中默认$R=50$,也就是有50个模式不同的分组。这里所谓的细胞类型分组其实就是组织空间上不同的区域或者域,模式值得就是这些分组在空间上的表达模式不同,而整个组织空间上的基因表达就是所有的这些域的基因表达的叠加组成的。我们也可以从图像作为例子,每一个域就像是图像的一个通道,最终我们看到的图像是所有通道信息的叠加。这也是和直观上理解的解卷积非常不一样的一点:直观上我们认为一个spot里的基因表达就是许多细胞类型的加权和,但作者认为一个spot的基因表达是多个域在这个spot上表达的加权和,而每个域中可能包括了多个细胞类型,一个细胞类型也有可能属于多个域。
于是在这样的层次结构下,作者又引入了两个重要参数$z_{s, r}$和$x_{r, f}$。其中$z_{s, r}$表示组$r$在不同位置的丰度,而和它相乘的是参数$x_{r,f}$,代表每个细胞类型对组r的贡献,相乘后再对r求和,我们就得到了细胞类型在不同位置的绝对丰度。下面我们分别来看
组$r$在不同位置的丰度:参数$z_{s, r}$
作者认为这个参数仍然服从Gamma分布:
$$
z_{s, r} \sim \operatorname{Gamma}\left(B_{s} / R, 1 /\left(N_{s} / B_{s}\right)\right) \qquad (6)
$$
这里的$N_s$是在空间位置$s$上的平均细胞总数,而$B_s$是在这个位置上期望出现的组的个数。这两个参数分别又服从Gamma分布,
$$
\begin{gathered}
N_{s} \sim \operatorname{Gamma}\left(\hat{N} \cdot v^{n}, v^{n}\right) \qquad (7)\\
B_{s} \sim \operatorname{Gamma}(\hat{B}, 1) \qquad (8)
\end{gathered}
$$
这里的$\hat{N}$是用户定义的每个空间位置上期望得到的细胞数,这可以由空间转录组配套的影像进行细胞核分割计数得到,而$\hat{B}$是每个位置期望的得到的组数,也是一个超参数,默认规定为7。
每个细胞类型对组r的贡献:参数$x_{r,f}$
仍然服从Gamma分布:
$$
x_{r, f} \sim \operatorname{Gamma}\left(K_{r} / R, K_{r}\right) \qquad (9)
$$
这里的$K_{r}$表示组r包含的细胞类型个数,这是不可知的。我们求一下分布的均值可以发现等于$1/R$,这也保证了$\sum_{r} x_{r, f}=1$。那么$K_{r} $也是服从Gamma分布的:
$$
K_{r} \sim \operatorname{Gamma}(\hat{A} / \hat{B}, 1) \qquad (10)
$$
这里$\hat{A} $是超参数,代表每个位置期望的细胞类型,默认为7。而$\hat{B}$前面介绍过了,是7。
至此,对于均值\mu_{s,g}的所有层次概率先验就介绍完毕了。
基因特异的尺度因子$m_g$
作者仍然用了层次的先验概率进行建模,首先是服从Gamma分布。
$$m_{g} \sim \operatorname{Gamma}\left(\alpha^{m}, \alpha^{m} / \mu^{m}\right)$$
然后又是多层次的先验分布。说实话这里我不太明白为什么需要建立这么多层次,似乎从原理上并不是很好解释。还是说这是统计上的某种标准动作?
$$
\begin{gathered}
\alpha^{m}=1 /\left(o^{m}\right)^{2} \\
o^{m} \sim \text { Exponential }(3) \\
\mu^{m} \sim \operatorname{Gamma}(1,1)
\end{gathered}
$$
位置特异的检测效率因子$y_s$
首先还是服从Gamma分布,其中的参数$\alpha^y$是用户决定的参数。
$$
y_{s} \sim \operatorname{Gamma}\left(\alpha^{y}, \alpha^{y} / y_{e}\right)
$$
而$y_e$代表不同batch的影响,服从另一个Gamma分布
$$
y_{e} \sim \operatorname{Gamma}\left(10,10 / \mu^{y}\right)
$$
其中的参数$\mu^{y}$用以下公式求得:
$$
\mu^{y}=\frac{\frac{\sum_{s} \sum_{g} d_{s, g} / S}{\hat{N}}}{\sum_{f} \sum_{g} g_{f, g} / F}
$$
其中分子代表空间上每个位置中每个细胞期望的总counts数,而分母为单细胞测序中平均每个细胞的总counts数。
基因加性噪声$s_{e,g}$
这里层次建模的思路是考虑到每个基因在不同batch下的影响是不同的,而代表batch信息的参数又服从固定的gamma分布。
$$
\begin{gathered}
s_{e, g} \sim \operatorname{Gamma}\left(\alpha_{e}^{s}, \alpha_{e}^{s} / \mu_{e}^{s}\right) \\
\mu_{e}^{s} \sim \operatorname{Gamma}(1,100) \\
\alpha_{e}^{s}=1 / o_{e}^{2} \\
o_{e} \sim \operatorname{Exponential}\left(\beta^{s}\right) \\
\beta^{s} \sim \operatorname{Gamma}(9,3)
\end{gathered}
$$
dispersion参数$\alpha_{e,g}$
对于这个参数作者说参考了文献《A Principled, Practical Approach to Constructing Priors. en. Statistical Science》,定义的方法仍然是多层概率图,其中的超参数9和3作者说是通过先前的数据观察到的:
$$
\begin{gathered}
\alpha_{e, g}=1 / o_{e, g}^{2} \\
o_{e, g} \sim \operatorname{Exponential}\left(\beta^{o}\right) \\
\beta^{o} \sim \operatorname{Gamma}(9,3)
\end{gathered}
$$
至此,整个概率图模型就介绍完毕了,我们再回来看这一幅图:

是不是感觉清晰了许多,从可观测的空间基因表达值$d_{s,g}$出发,一层层的建立出先验分布,刻画出最关键的$w_{s,f}$和$z_{s,r}$。
模型构建出后该怎么优化呢?作者提到了用pyro包可以进行自动变分,然后就可以求出来所有参数了。
我在读完这个方法的几个疑问是:
- 这么多层次的概率图模型到底是如何构建的?
- 这么多参数的消融实验该如何设计?怎么能证明当前模型是最优的呢?那为什么不给上图的每个超参数再加一层先验分布?
- 具体的优化从代码上是如何实现的?
都看到这里了,不点赞或者打赏再走吗?
看情况日后可能会更新这篇文章对于仿真数据的设计,也比较有新意。
文章评论